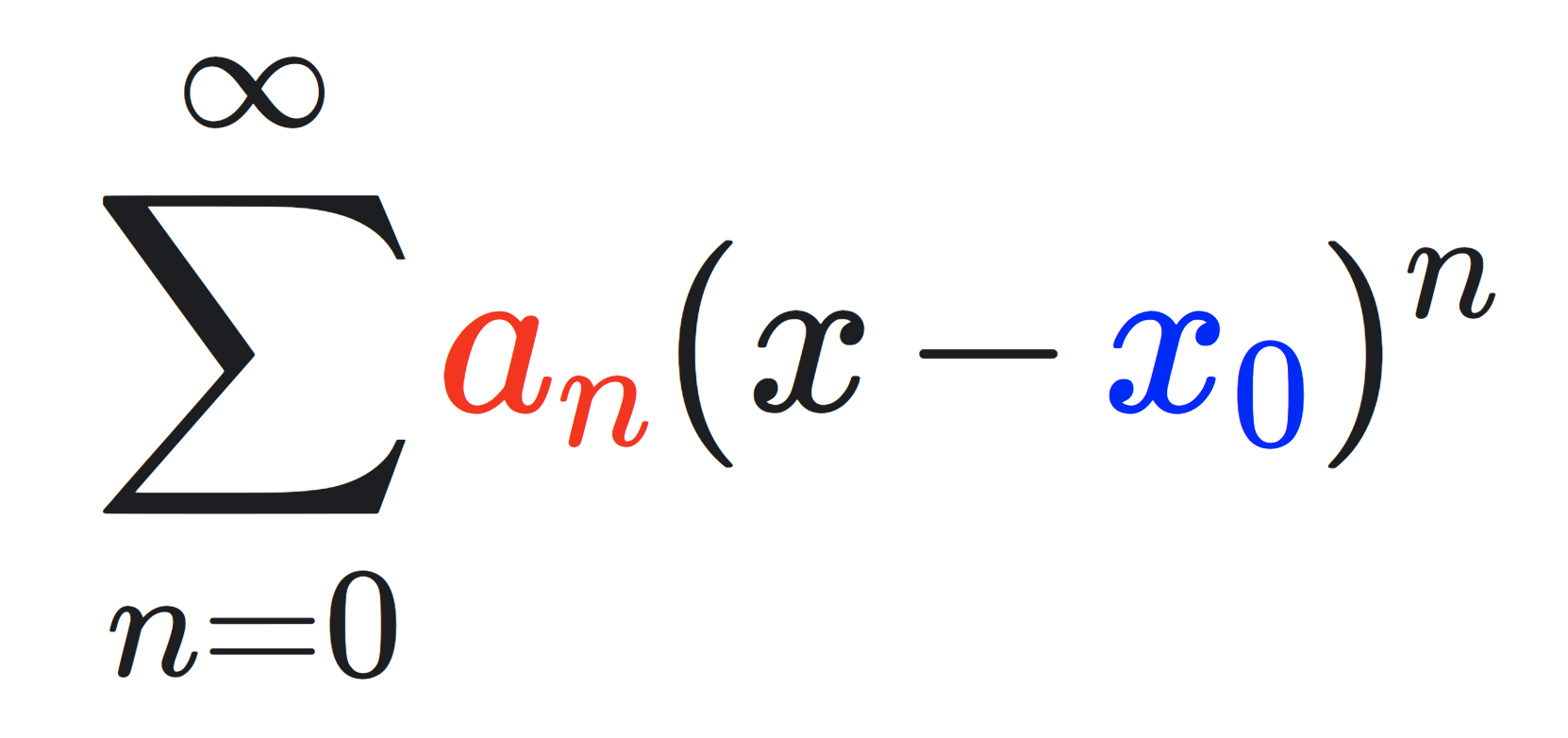 다양한 급수
다양한 급수
급수(級數)는 수열의 모든 항을 더한 값입니다.
여기에서는 무한한 항의 합인 무한급수 에 대해 다룹니다.
멱급수
멱급수 또는 거듭제곱 급수(Power series)는 주어진 변수를 거듭제곱한 항들의 무한급수이자,
중심이 같은 멱함수를 항으로 하는 무한급수입니다.
실수체 또는 복소수체 K∈{R,C}에서 중심 x0∈K의 멱급수는 다음과 같이 정의됩니다.
n=0∑∞an(x−x0)n 자세히 살펴보면 등차수열an과 등비수열(x−x0)n로 이루어져 있습니다.
이 멱급수가 수렴하게 만드는 x∈K의 집합을 멱급수의 수렴영역(domain of convergence)이라고 합니다.
실수 영역에선 수렴구간(interval of convergence)
복소수 영역에선 수렴원판(disc of convergence)라고 구분하기도 합니다.
테일러 급수
테일러 급수(Taylor series) 또는 테일러 전개(Taylor expansion)는 도함수들의 한 점에서 계산된 항의 무한합으로 해석함수를 나타냅니다.
복잡한 함수를 다루기 쉬운 다항함수로 바꿔줌으로써, 정적분의 값을 근사적으로 구할 수 있습니다.
매끄러운 함수(Smooth function) f:R→R 및 실수 a∈R
(또는, 복소수계의 정칙함수)이 주어졌을 때,
f의 테일러 급수는 다음과 같이 정의됩니다.
f(x)=n=0∑∞n!f(n)(x0)(x−x0)n 여기에서 f(n)(x0)는 f의 x0에서 n계 도함수를 말합니다.
특히 0계 도함수는 원래 함수 자신입니다.
테일러 급수는 오차를 가지고 있습니다.
k=0∑nk!f(k)(x0)(x−x0)k+Rn+1(x) 마지막 항인 Rn+1(x)을 f의 나머지 항 또는 절단오차라고 합니다.
[x0,x] 또는 [x,x0]에 속하는 적당한 실수 b에 대해서 다음과 같이 표현됩니다.
Rn+1(x)=(n+1)!f(n+1)(b)(x−x0)n+1 이 오차가 0으로 원래 함수로 수렴하는 경우 해석 함수라고 합니다.
테일러 전개
다항식이 아닌 함수를 테일러 급수로 만들어 봅시다.
예를 들어 자연상수 e의 거듭제곱
an=n!f(n)(x0) 를 살펴봅시다.
ex를 무한개의 항을 가진 다항식으로 가정하면,
ex=a0+a1x+a2x2+a3x3+a4x4+... 입니다.
a0를 계산해 볼까요? a0=0!f(0)=e0=1 이므로,
ex=1+a1x+a2x2+a+3x3+a4x4+... 다항식을 미분하면
ex=a1+a22x+a33x2+a44x3+... 입니다.
a1도 계산해 봅시다. a1=1!f′(0)=1 이므로
ex=1+2a2x+3a3x2+4a4x3+... 다항식을 미분하면
ex=2∗a2+(2∗3)a3x+(4∗3)a4x2+... 마찬가지로 a2=2!f′′(0)이고 an=n!1임을 알 수 있습니다.
따라서 ex는 처음 식에서
ex=1+x+2!x2+3!x3+4!x4+... 로 테일러 전개 되는 것을 알 수 있습니다.
매클로린 급수
x0=0일 때의 테일러 급수를 매클로린 급수라고 합니다.
f(x)=n=0∑∞n!f(n)(0)xn 모든 다항식에서 매클로린 급수는 다항식 자기 자신이 됩니다.
이항급수
복소수 a∈C가 주어졌을 때, 이항급수는 (1+x)α의 매클로린 급수입니다.
f(x)=n=0∑∞n!(α)kxn 여기서 (α)k는 조합(combination)에서 하강계승입니다.
자세한 내용은 이항정리를 참고해 주세요.
References
[wiki]멱급수
[wiki]테일러 급수
[wiki]매클로린 급수
[wiki]이항 급수
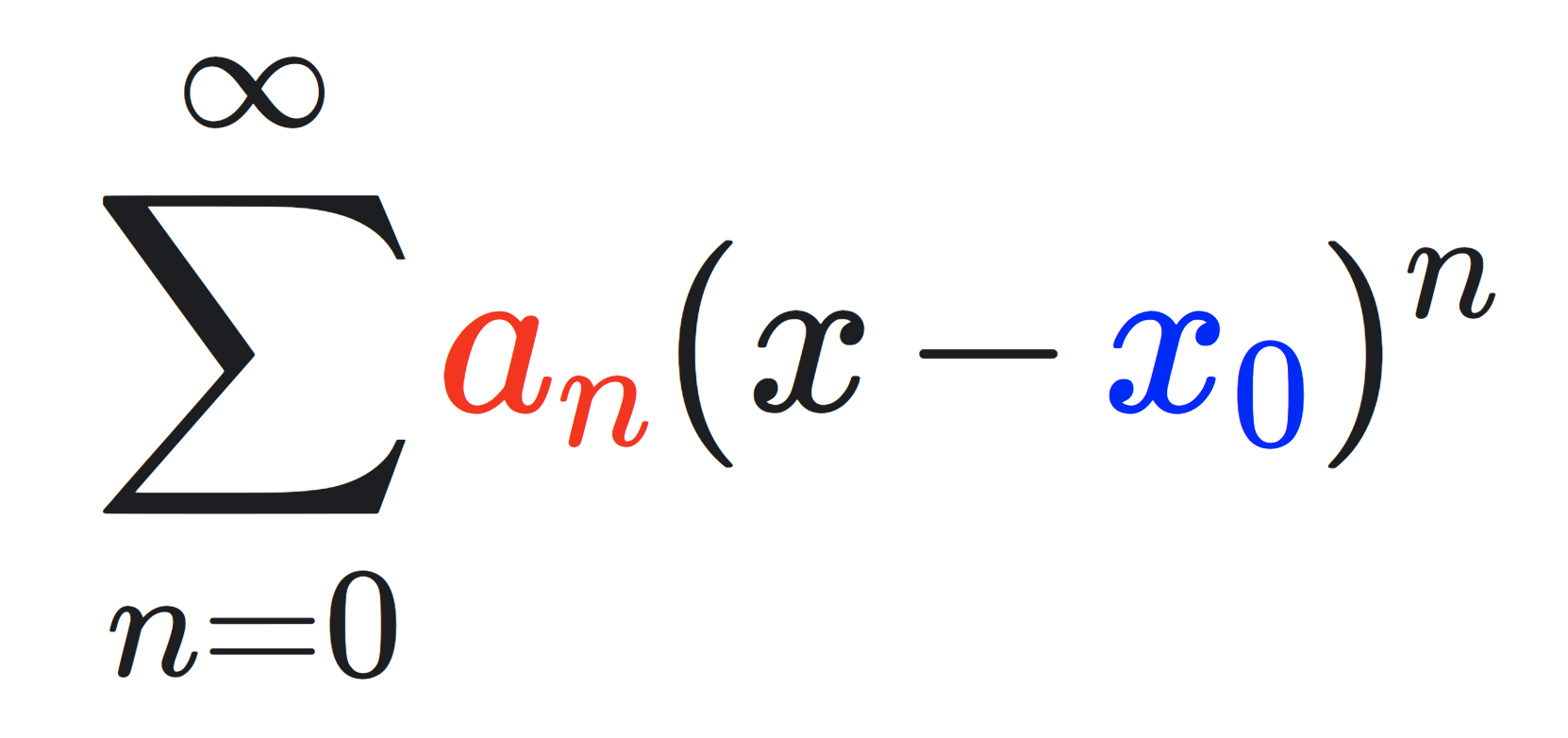 다양한 급수
다양한 급수
