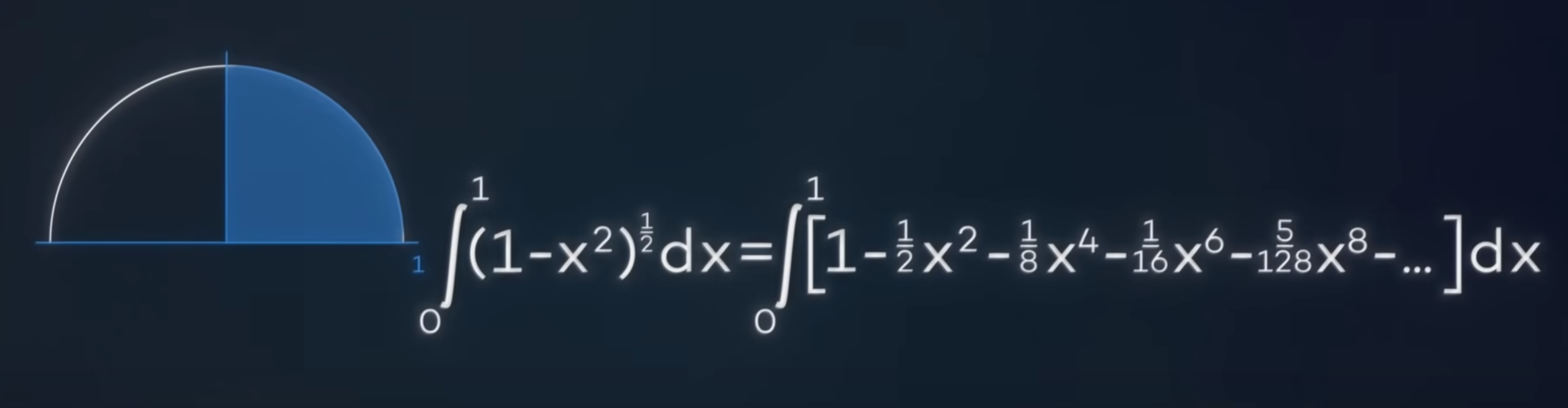이항정리 - π값을 구하는 법
π
여러분은 π값을 알고 계신가요?
π는 원의 반지름과 둘레의 비율을 나타내는 값으로,
3.14 언저리의 값이라는 것을 알고 계실겁니다.
π Day

[트위터]파이데이
동영상에서 보듯이, 피자의 둘레를 펴 지름에 놓으면 3판보다 조금 더 큰 것을 알 수 있습니다.
그렇다면 파이값을 어떻게 구할 수 있을까요?
고대인들도 π값을 알고 있었습니다.

한 변의 길이가 1인 육각형의 둘레는 6입니다.
육각형에 외접원을 그리면, 육각형보다 큰 원을 그릴 수 있습니다.
같은 지름을 공유하는 원의 둘레가 더 크므로, 다음 부등식을 세울 수 있습니다.
(원의둘레)=(지름)∗π=2π>6 양변을 2로 나누면,
π 값은 3보다 크다는걸 알았습니다!

한 변의 길이가 2인 사각형은 둘레가 8로, 이전에 그렸던 도형보다 큽니다.
사각형의 둘레가 더 크므로, 다음 부등식을 세울 수 있습니다.
양변을 2로 나누면,
π는 4보다 작은 값임을 알아냈습니다!
이렇게 다각형을 이용해 근사하는 방법은 2200년전, BC 250년에 아르키메데스가 계산한 방법으로,
내접, 외접한 다각형의 변을 늘려가며 더 정확한 근사치를 구할 수 있습니다.
이 방법은 1000년간 π 값을 구하는 방법으로 사용되었습니다.
71223<π<722 3.1408<π<3.1429 정구십육각형
사실 이정도만 되어도 실용적인 정확도를 넘어섭니다.
1850년, William Shanks는 15년간 π값을 계산해 707자리까지 계산합니다.
하지만 527자리부터 오류가 있었죠. 이걸 계산하는데 사용한 사간은 아무것도 아닌 것에 낭비된 것 처럼 보입니다.
이 외에도 π값을 구하는 방법은 Monte Carlo Simulation,
Buffon’s Needles 등 방법이 있지만,
지금 다룰 진짜 주제는 π가 아니니 넘어가겠습니다.
적분의 등장
뉴턴과 라이프니츠는 17세기 미적분학의 기본정리를 완성합니다.
미분과 적분이 서로 역연산관계에 있습니다.
정적분은 부정적분의 차로 구할 수 있습니다.
정적분 값을 계산할수 있게 되면서 π 값을 구하는 방법은 변하게 됩니다.
이전까지는 (원의둘레)=2∗π를 이용했다면,
이제부터는 (원의넓이)=r2∗π을 이용하게 됩니다.
원의 넓이1
좌표계에서 단위원의 방정식 x2+y2=1을 나타내면 다음과 같습니다

적분가능한 함수 y=(1−x2)21로 나타내면

어떻게 적분할 수 있을까요?
안타깝게도, 지금 알고있는 지식으로는 적분할수 없습니다.
그래도 궁금하신 분을 위해
이 식의 부정적분은 다음과 같습니다.
∫(1−x2)=21(1−x2)21x+sin(x)−1+c 이항정리
위의 식을 적분하려면, 이항정리와 이항계수를 알아야 합니다.
이항식은, 두 단항식의 합인 다항식을 말합니다.
이항정리는, 이항식의 거듭제곱 (x+y)n을 단항식axbyc들의 합으로 전개하는 정리입니다.
(x+y)n=k=0∑n(nk)xn−kyk=xn+nxn−1y+2n(n−1)xn−1y2+...+axbyc+...+yn 여기에서 b+c=n이고, 단항식의 계수a는 이항계수라고 불리고
a=(nb)=(nc)입니다.
n choose b 또는 n개에서 b개를 고르는 조합으로 읽습니다
이항계수(binomial coefficient)
직접 이항식 (x+1)의 거듭제곱을 계산해 볼까요?
(1+x)0=1(1+x)1=1+x(1+x)2=1+2x+x2(1+x)3=1+3x+3x2+x3(1+x)4=1+4x+6x2+4x3+x4 눈치 빠르신 분이라면 (1+x)n이 어떤 형태인지 추측하셨을 겁니다.
위에서 설명했듯이, n항식의 k항의 계수는 조합 (nk)=k!(n−k)!n!
또는, k!Πi=0k−1(n−i)와 같습니다.
조합수는 pascal's triangle에서 찾을 수 있습니다.
n=0n=1n=2n=3n=4111121133114641 이항계수를 구할때, 대수학으로 계산하는 대신 조합수를 사용해 편리하게 계산할 수 있습니다.
일반화된 이항정리
이항식을 거듭제곱하는 지수를 임의의 복소수 α∈C 까지 확장할 수 있습니다. 일반화된 이항 정리에선 전개가 무한급수가 됩니다.
natural numbers(N) - integers(Z) - rational(Q) - real(R) - complex(C)
음이향계수
음수일때 계승! 은 정의되지 않지만, 다음과 같이 계산합시다.
−1!=−1×−2×−3×−4...−2!=−2×−3×−4...−3!=−3×−4... -1차식의 0항의 계수는
(−10)=0!−1!−1!=1
-1차식의 1항의 계수는
(−11)=1!−2!−1!=−1
-1차식의 2항의 계수는
(−12)=2!−3!−1!=1
...
-2차식의 0항의 계수는
(−20)=0!−2!−2!=1
-2차식의 1항의 계수는
(−21)=1!−3!−2!=−2
-2차식의 2항의 계수는
(−22)=2!−4!−2!=3
...
위의 계산을 일반화하면
(−rk)=k!(−r)(−r−1)...(−r−k+1)=(−1)kk!(r)(r+1)...(r+k−1)=(−1)k(r+k−1k) 음이항계수를 파스칼의 삼각형에 이어서 그려볼까요?
n=−4n=−3n=−2n=−1n=0n=1n=2n=3n=41−4...1−36...1−23−4...1−11−11...111121133114641 분수계수
이항계수는 분수일 때도 정의할 수 있습니다.
21에서 이항계수를 살펴봅시다.
21차식의 0항의 계수는
(210)=0!21!21!=1
21차식의 1항의 계수는
(211)=1!−21!21!=21
21차식의 2항의 계수는
(212)=2!−23!21!=2!−41=−81
...
원의 넓이2
이항식의 분수 거듭제곱에서 이항계수를 구하는 법을 알았으니,
(1−x2)21식을 전개할 수 있습니다!
편의를 위해 −x2=t로 놓으면,
(1+t)21=1+21t−81t2+161t3−... 다시 x에 대해서로 바꿔줍시다
(1−x2)21=1−21x2−81x4−161x6−... [0,1] 구간의 정적분을 구하면
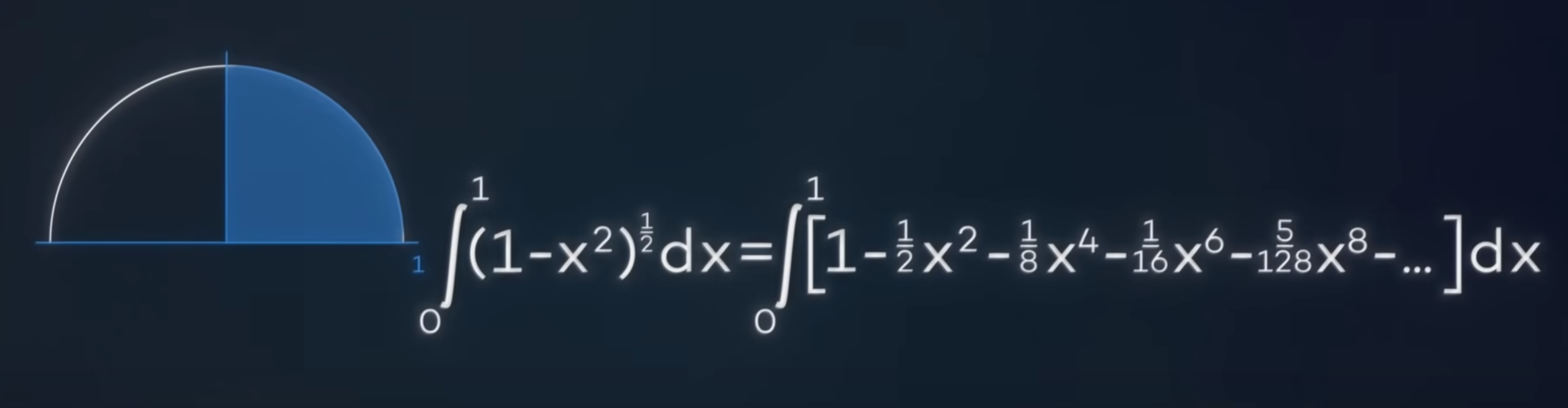
이 값은 무한히 전개되므로 전부 계산할 수 없습니다.
하지만 원의 넓이 π의 1/4, π/4를 나타낸다는 것을 알고 있습니다.
4π=∫01[1−21x2−81x4−161x6−...]dx=[x−61x3−401x5−1121x7−...]01=672533=0.79315476190 위 식을 네번째 항까지 계산한 π 값은 3.172619047 입니다!
다섯째 항까지 계산하면 4x(6361/8064)=3.15525793650로 점점 정확해짐을 알 수 있습니다
원의 넓이3
정적분의 범위를 [0, 1/2]로 설정하면 정적분의 값을 더 빠르게 구할 수 있습니다.
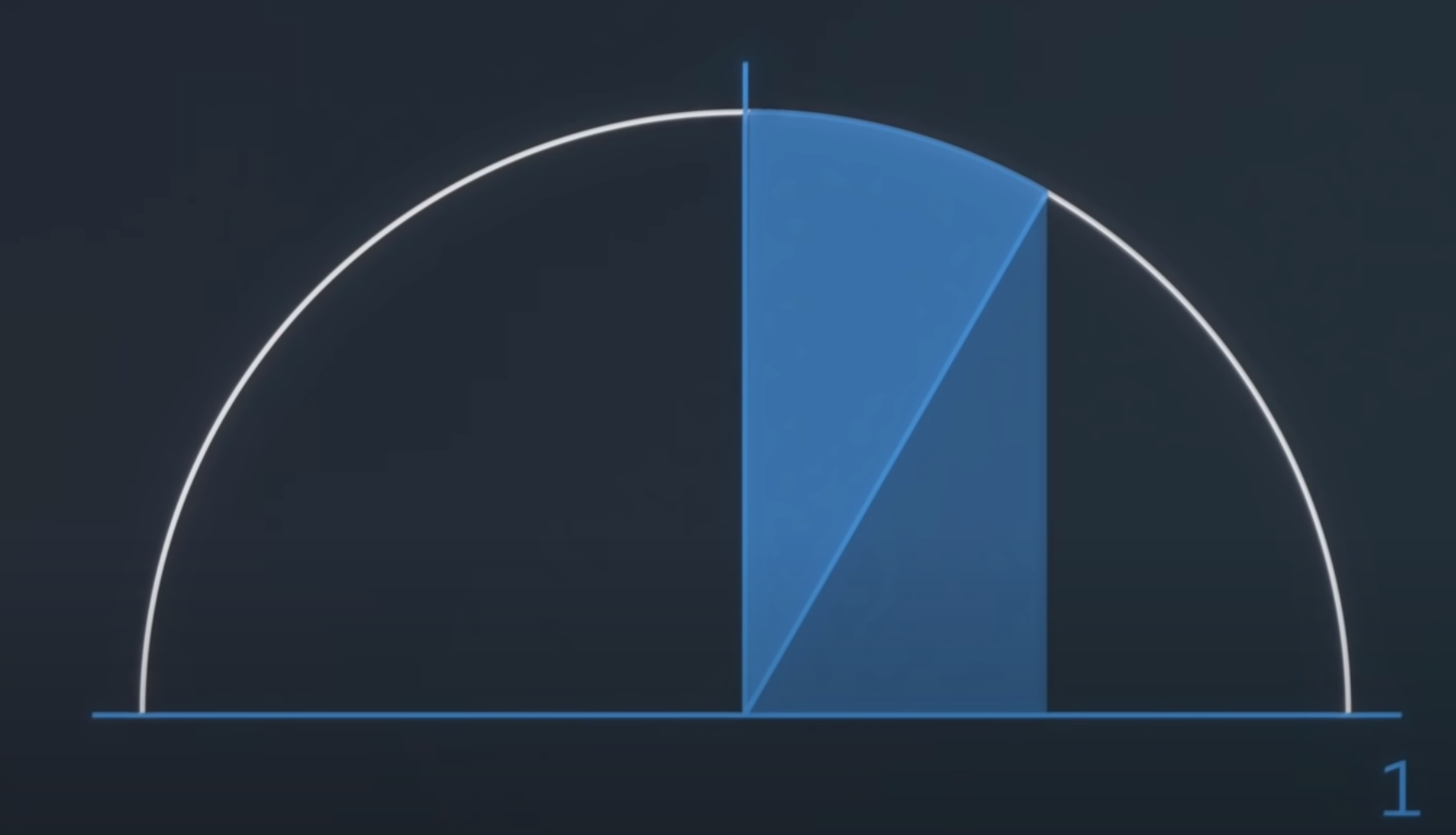
피타고라스와 삼각함수 덕에 이 넓이는 쉽게 알 수 있습니다.
밑변의 길이가 1/2이고 빗변이 1인 삼각형은 사이각이 60도 입니다.
따라서, 이 부분의 넓이는 원의 넓이 π의 12분의 1인 원뿔과
밑변이 21, 높이가 23인 삼격형 넓이의 합입니다.
12π+83 정적분과 이항정리를 통한 다항식의 전개로 π를 계산하는 방법은 뉴턴이 제안했습니다.
아르키메데스의 방법과 정확도를 비교해보면,
4천조(兆)각형을 계산할 때와 뉴턴 급수의 50개의 항을 계산했을때가 같습니다.
References
[위키]원주율
[위키]이항정리
Calculating Pi
π를 계산하는 특별한 방법